저장소
[암호학] 3.11 finite fields(유한체) 본문
유한체는 암호학의 여러 분야에서 중요하게 사용된다.
유한체
- 유한개의 원소를 가지는 체
- GF(p^n): p^n개의 원소를 갖는 유한체 (p = 위수, n = 자연수)
- 유한체의 위수는 n이 양이 정수일 때, 소인수의 멱승(어떤 수 또는 식에서 그 거듭제곱을 구하는 계산법)인 p^n
- 갈루아 체: 갈루아가 원소들의 개수가 p^n인 유한개의 원소를 갖는 체가 존재함을 보임
- 유한체 집합 내 원소의 연산(덧셈, 곱셈)의 결과가 그 집합 내에 존재함
- GF(p) -> Prime Field, GF(2^n) -> Binary Field
위수 p 유한체
- 소수 p에 대해서 위수가 p인 유한체 GF(p)는 정수 {0, 1, ..., p-1}의 집합 Z_p로 정의된다. => 원소에 모듈러 p의 산술 연산이 수행됨
- Z_p상의 0이 아닌 모든 정수들에 대하여 곱셈 역원이 존재한다.
- GF(p)의 각 원소에 대한 곱셈의 역원은 확장 유클리드 호제법을 사용하여 계산이 가능하다.
- Z_n의 모듈러 연산 속성은 아래와 같다.
- 교환법칙
- 결합법칙
- 분배법칙
- 항등
- 덧셈에 대한 역원
- 곱셈에 대한 역원
산술 다항식
하나의 미지수 x를 갖는 다항식들이 존재하는 경우 산술 다항식은 3가지
- 대수의 기본 규칙을 따르는 일반적인 산술 다항식
- GF(p) 유한체 내의 원소들을 다항식의 계수로 사용하고 각 계수들은 모듈러 p 연산으로 수행되는 산술 다항식
- GF(p) 유한체 내의 원소들을 다항식의 계수로 사용하고, 최고차항이 n인 다항식 m(x)의 모듈러 연산으로 수행되는 산술 다항식
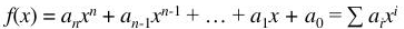
=> 일반적인 산술 다항식은 덧셈/뺄셈/곱셈 연산들이 가능함 (덧셈/뺄셈은 두 다항식에서의 대응 계수를 더하거나 빼는 것을 의미)
Z_p의 계수를 이용한 산술 다항식
- 체 F의 다항식: 체 F의 원소들을 계수로 갖는 다항식
=> 각각의 다항식을 원소로 갖는 집합은 환을 형성 -> 다항식 환이라고 함
- 산술 다항식이 체에서 수행되는 경우 나눗셈 연산이 가능함
- n차 다항식 f(x)와 m차 다항식 g(x)가 존재할 경우 f(x) = q(x)*g(x) + r(x)로 표현 가능
Ex) GF(2) 연산
f(x) = x^3 + x^2이고 g(x) = x^2 + x + 1이면
-> f(x) + g(x) = x^3 + x + 1
-> f(x)g(x) = x^5 + 3x^2 - 2x + 2
처럼 산술 연산이 가능함
- 다항식에서 gcd[a(x), b(x)]는 a(x)와 b(x)를 모두 나눌 수 있는 최대 차수의 다항식을 의미함
=> 유클리드 호제법을 사용하여 구할 수 있음
GF(2^n) 유한체
- 산술연산을 효율적으로 구현하기 위해 정수를 사용(n bit word 표현을 위해 0 ~ 2^n-1 범위 정수 사용)
- 모듈러 다항식 연산을 통해 원소들을 사용하여 p^n개의 서로 다른 다항식을 만들 수 있음
- 2^n개의 원소들로 구성
- GF(2^n)의 원소들로 이루어진 집합에는 덧셈, 곱셈 같은 2항 연산자가 정의되어 덧셈, 곱셈, 나눗셈 등의 연산을 동일 집합 내에서 수행할 수 있음 + 0이 아닌 모든 원소들은 곱셈에 대한 역원 존재
- GF(2^n) 모든 원소들은 n – 1 또는 그보다 작은 차수의 다항식으로 이루어진 집합으로 정의할 수 있으며, 각각의 다항식들은 n비트의 이진수로 표현이 가능함
- GF(2^n)의 원소들은 n차 기약 다항식의 모듈러 연산으로 계산될 수 있으며, 생성자와 생성자의 거듭제곱 값들을 이용하여 GF(2^n)상에서 동형의 유한체를 정의할 수 있음
산술연산 정의
- 계수들 간의 산술연산은 모듈러 p로 수행
- 유한체 Z_p상의 산술규칙을 이용
계산
- GF(2^n)상의 다항식 f(x)는 n개의 0 or 1로 표현되는 이진계수를 통해 표현됨
- GF(2^n)상에서의 모든 다항식은 n비트의 숫자로 표현 가능함
덧셈
- 같은 차수의 계수를 더함으로써 다항식들의 덧셈 연산을 수행
- Z_2 기반의 다항식 덧셈은 XOR 연산과 동일함
곱셈
- GF(2^n)의 곱셈 연산은 단순한 XOR 연산으로는 수행 불가능
- AES에서 사용되는 GF(2^8)상의 유한체의 경우 특정 식을 반복적으로 수행하여 높은 차수의 x를 곱한 결과를 얻을 수 있음
LFSR(Linear Feedback Shift Register)
스트림 암호의 난수를 생성하는 용도로 많이 쓰임
일반적으로 XOR 연산을 사용함
http://www.secmem.org/blog/2019/08/19/Linear-Feedback-Shift-Register/
Linear Feedback Shift Register
안녕하세요, 이번 글에서는 Linear Feedback Shift Register에 대해 알아보도록 하겠습니다. Linear Feedback Shift Register Linear Feedback Shift Register(a.k.a LFSR)는 현재 상태에서의 선형 연산을 통해 다음 상태를 생
www.secmem.org
'IT > 암호학·블록체인' 카테고리의 다른 글
| [암호학] 7.5 The ElGamal Public Key Cryptosystem (0) | 2021.08.27 |
|---|---|
| [암호학] 7.4 Diffie-Hellman Key Exchange (0) | 2021.08.27 |
| [암호학] 6.1 The RSA Algorithm (RSA 알고리즘) (0) | 2021.08.20 |
Comments


